When a particle is incident upon a potential barrier of height U, its wave function ψ(x) predicts the probability that it will tunnel through the barrier. For electrons in solid state materials tunneling across a vacuum gap to or from a metallic electrode, the tunneling probability is exponentially dependent on the gap. The solution to the time-independent Schrodinger equation of a simplified 1-D model of tunneling across a vacuum barrier of width  is:

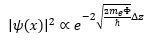
 where  φ = U - E is the work function of the material, and  is the electron energy. A bias voltage V_bias across the barrier results in a sustained tunneling current. The Bardeen model for tunneling gives a tunneling current:

 , 

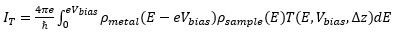where ρ_metal and ρ_sample are the electronic densities of states of the metal electrode and sample, respectively.  T(E,V_bias,Δz) is the transmission probability at electron energy E. For sufficiently small bias voltages and constant metallic density of states, the differential conductance is proportional to the sample density of states:

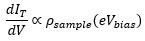
In practice, the metallic electrode can be fashioned into a sharp tip to probe the local electronic density of states anywhere on the sample surface. The scanning tunneling microscope (STM) is a device designed in this way that can also raster scan the surface and achieve high resolution imaging. When the STM tip is fixed, however, it is still able to perform interesting science: observation of the exponential dependence of the tunneling current on the tip-sample spacing (Δz) and information about the electronic density of states from the differential tunneling conductance (dI/dV)

A simpler device that can perform these measurements is the z-Axis Tunneling Microscope (ZTM). The ZTM limits tip motion to the z-axis (tip-sample separation), using a single piezo stack as the actuator. Absent are the x-y scanners and feedback loop present in the STM.

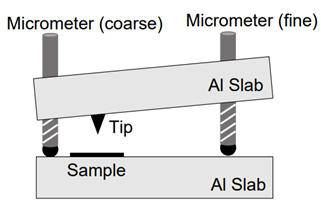The tip and sample are placed near the pivot of a two-slab approach body, using the mechanical advantage to slow the approach. The tip needs to be brought to within 1 nm of the surface without crashing. A stepper motor advances the fine micrometer screw. After each step, the z-piezo stack extends to search for the sample. A small current-voltage pre-amplifier circuit—capable of detecting tunneling currents as small as 10 pA—is attached to the top slab. In experiments, the current is recorded while sweeping either the bias voltage (I-V) or the piezo voltage (I - Δz). The device can be plugged in to existing college/university infrastructure. We use NI DAQ devices controlled by LabVIEW to apply bias voltage, apply piezo voltage, and sense tunneling current.

 

The simplification and cost savings expand access to more undergraduate students interested in studying electronic tunneling and electronic structure. The device allows more experimentation in solid state physics at the undergraduate level. Students can observe the exponential dependence of the tunneling barrier width, measure the material work function, and obtain local electronic density of states data to observe qualitative differences in metals, semiconductors, and more. Students can also gain experimental skills familiar to the condensed matter physicist: I-V acquisition, noise reduction demands for pA-nA currents, vibration isolation, and signal processing. Advanced students could acquire dI/dV directly via a lock-in amplifier. Programs that implement the ZTM with a software controller (i.e., LabVIEW) can use the data as impetus for student creation of signal processing programs.

 

The immersion will consist of three phases:

1.       Assembling the components of the ZTM body, cutting tips for tunneling, and discussing DAQ options. Considerations for safely approaching the tip depending on DAQ options.

2. I-V acquisition. Qualitative comparisons for different samples (for example: highly oriented pyrolytic graphite, Au, Si). Considerations for data processing.

3. I-Δz acquisition. Fitting and evaluating an exponential model to the data. Extracting the work function, and sources of systematic error in ambient conditions.

 

Cost of developing the experiment:

Samples and material costs for construction come to about $500. Adoptees may opt to use the device in existing DAQ infrastructure at their home institutions. The DAQ devices used at the immersion are approximately $6,000, but similar results may be achieved with DAQ devices costing as low as $400. The tradeoffs for the least expensive DAQ devices would be lower sampling rate and longer wait times to safely approach the tip. For those using LabVIEW, the controller VI used at the immersion can be taken back to their home institutions.

 

Host and Mentor:

Joshua Veazey is an assistant professor of physics at Grand Valley State University, where he teaches advanced lab and introductory physics. He received his Ph.D. in physics from Michigan State University, and his B.S. in physics from the University of Rochester. Josh’s research interests include electronic structure and electromechanical behavior of materials at the nanoscale. He enjoys involving undergraduate students in this research, and in the development of advanced lab apparatus.

Dr. Joshua Veazey, Email: veazeyj@gvsu.edu

Please note that the Jonathan F. Reichert Foundation has established a grant program to help purchase apparatus used in Laboratory Immersions. Limitations and exclusions apply, but generally speaking the Foundation may support up to 40% of the cost of the required equipment.